Las suspensiones de servicio eléctrico y los cambios bruscos de voltaje no sólo se producen debido a fallas en el sistema de transmisión de la energía, sino también por sobrecargas en las redes de distribución, que por lo general, se acentúan en invierno. Entre los factores que ponen en riesgo la continuidad y calidad del suministro se encuentran los incrementos de la demanda derivados de la sustracción de energía. Los afectados por el deterioro de la calidad del servicio son tanto los consumidores de electricidad como la empresa distribuidora de energía.
Introducción
Los efectos sobre los consumidores son numerosos: daños a los equipos eléctricos, imposibilidad de realizar el disfrute de estos mismos equipos, aumento de la inseguridad, etc. Por otro lado, las distribuidoras sufren pérdidas, las cuales tienen que pagar a los generadores por una energía que no es facturada y dependiendo del caso, deben afrontar sanciones producto del deterioro de la calidad del servicio. Consecuentemente, es del interés de las empresas distribuidoras el combatir tal delito.
En esta nota se analizará el proceso de decisión de una familia que evalúa conectarse clandestinamente, para lo cual se empleará un enfoque estratégico. Cada familia no toma esta decisión independientemente de las demás familias, sino que interactúa con otras familias. Una familia puede decidir no abonar la energía si considera que las demás sí lo harán y por lo tanto el servicio continuará brindándose, aunque sea con un nivel de calidad aceptable. El análisis será ilustrado empleando herramientas elementales de teoría de juegos, cuyo objetivo es precisamente el estudio de la toma de decisiones en contextos donde existe interacción estratégica entre varios agentes o jugadores.
En el análisis se plantearán dos situaciones diferentes. En primer lugar, se considerarán dos familias con similar poder adquisitivo y que pueden afrontar el pago del servicio; y en segundo término, dos familias que tienen diferentes niveles de ingresos.
Familias de ingresos similares Imagínese una sociedad compuesta sólo por dos familias, A y B. Cada familia debe consumir energía eléctrica para hacer funcionar sus artefactos eléctricos. Estas familias tienen similar poder adquisitivo, el cual les permitiría afrontar el pago del suministro eléctrico (Más adelante se comentará qué sucede si hay una familia que no puede afrontar el pago del servicio).
El servicio de distribución de energía eléctrica debe ser brindado por una empresa, la cual tiene sus tarifas reguladas. Sin embargo, tiene dificultad a la hora de controlar las pérdidas de energía. La empresa no puede distinguir si una pérdida es originada como consecuencia del fraude o de una pérdida técnica, por lo tanto no puede imponer una penalidad a aquella familia que no paga el servicio.
Dada esta imposibilidad de la empresa de controlar el fraude, las familias podrían evaluar la posibilidad de obtener la energía clandestinamente. Por lo tanto, cada familia debe decidir si paga por el servicio o defrauda. A partir de la decisión que tome cada familia se podrían tener cuatro resultados posibles:

Estos resultados se presentan gráficamente en la siguiente tabla:
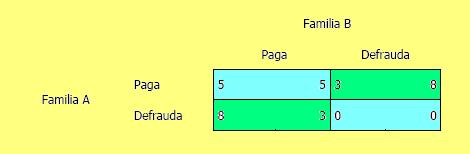
Los valores en cada celda indican la utilidad (No son necesariamente valores monetarios. Se trata de un índice de utilidad) que obtiene cada familia: el primer valor es la utilidad para la familia A y el segundo es la utilidad para la familia B.
Si ambas familias pagan obtienen un servicio de buena calidad, lo cual es valorado por cada una de ella en 5. Si ambas defraudan obtendrán 0 de utilidad: no podrán seguir gozando del servicio en el futuro ya que la empresa quebrará (alternativamente el servicio podría verse seriamente deteriorado).
Si A paga y B defrauda, A ve resentido en parte el servicio, pero puede seguir disfrutando de él; mientras que B se beneficia porque consigue un servicio que no paga. A pesar de que para B también disminuye la calidad del servicio, esta caída en la calidad del servicio no logra compensar la mejora en el bienestar que le implica no pagar el servicio (este ingreso “adicional” puede destinarlo al consumo en general). En el caso en que sea B quien paga y A la que defrauda, el análisis es el inverso.
¿Qué cabría esperar que suceda en esta sociedad? Se verá que la única situación que puede mantenerse es aquella en la que una familia paga y la otra defrauda. Analícese primero qué sucede si ambas pagan. Por ejemplo, si A supone que B paga el servicio, lo mejor que puede hacer es no pagar porque sus utilidades pasan de 5 a 8. Cada familia tiene incentivos a defraudar. Pero el caso en que ambas defraudan tampoco es sostenible. Si ninguna está pagando, dado que una familia no paga la otra preferiría comenzar a pagar, porque así su utilidad sería de 3 y no de 0.
La única situación que es sostenible es aquella en que una familia paga y la otra no.
Supóngase que es A quien paga y B la que defrauda. Si A se decidiera a no pagar su utilidad caería de 3 a 0. En cambio, si B comenzara a pagar, su utilidad disminuiría de 8 a 5.
Pero se tendrían dos soluciones posibles. ¿Cuál será la familia que pague y cuál la que cometa fraude? No es mucho lo que se puede decir con los elementos que se han introducido hasta aquí. Dependerá de factores socio-económicos que no se han señalado y de la dinámica de la interacción social. Se podría pensar que inicialmente ambas familias pagaban, en cuyo caso el “premio” sería para la familia que dejara de pagar primero. Esta familia sería la primera que percibiera la imposibilidad de la empresa para castigar el fraude o aquella que pudiera correr el riesgo de quedarse sin el servicio en caso de que todas dejen de pagar o aquella familia que no tiene una “imagen” social que cuidar. De hecho estos factores son los que caracterizarían a las familias que pudiendo pagar por el servicio optan por cometer fraude.
Si se considerara una sociedad más numerosa, los resultados serían similares. Habría un número mínimo de familias que deberían pagar por el servicio para que éste sea sostenible. Si a partir de este número mínimo, hubiera más familias que decidieran no pagar, el servicio dejaría de brindarse.
Sociedad con una distribución desigual del ingreso
En los hechos, sin embargo, la distribución de los ingresos no es homogénea, existiendo familias por debajo de la línea de pobreza. Estas familias pueden, como en el caso anterior, valorar la posibilidad de obtener la energía de forma ilegal. Se podría ilustrar el caso en que coexisten una familia pobre y una no pobre mediante la siguiente tabla:
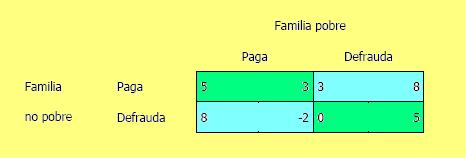
En este caso lo único que ha cambiado es la utilidad que percibe la familia de menores ingresos. Como puede observarse, debido a su restricción presupuestaria, prefiere defraudar independientemente de lo que haga la familia no pobre dado que puede destinar el ingreso “adicional” a satisfacer necesidades básicas. Indudablemente, la familia pobre si no paga prefiere que la otra familia pague (obteniendo un servicio de calidad aceptable) a que no pague (con lo que el servicio sería de mala calidad). La peor situación para la familia pobre es aquella en la que ella paga y la no pobre defrauda, porque por un lado obtiene un servicio de menor calidad que el que está abonando y por otro lado porque sacrifica consumo de bienes indispensables.
El análisis de las diferentes alternativas se realiza de la misma forma que en el ejemplo anterior. Sin embargo, la única situación sostenible es aquella en que la familia no pobre paga y la pobre defrauda. En efecto, dado que la familia no pobre sabe que la familia pobre prefiere defraudar optará por pagar dado que de esta forma obtiene un servicio de calidad aceptable.
Conclusiones
El análisis anterior se ha basado en grandes simplificaciones de la realidad. Las conclusiones serían diferentes si la empresa distribuidora cumpliera un rol más activo y pudiera controlar el fraude (aunque fuera de manera imperfecta). En este caso las familias deberían evaluar, en el momento de tomar una decisión, el riesgo de ser descubiertas hurtando la energía y las consiguientes sanciones que esta conducta les acarrearía. Por otro lado, se podrían diseñar mecanismos que incentiven a las familias a pagar por el servicio; por ejemplo: otorgar descuentos en la facturación a quienes cumplan regularmente con el pago del servicio.
Por otro lado, en la elaboración de los ejemplos se han considerado sólo factores económicos. Si las familias consideraran que existen “penalizaciones” extra económicas en caso de conectarse clandestinamente, se podría llegar a un resultado en el que no existirían incentivos a defraudar, con lo que toda la sociedad pagaría por el servicio que consume.
Como conclusiones de lo analizado se señala que, bajo determinados supuestos, un grupo de familias puede tener incentivos a no pagar por el servicio eléctrico a pesar de contar con ingresos suficientes. Por otro lado, la existencia de familias de bajos ingresos puede implicar que sólo las familias de mayores ingresos afronten el servicio, con lo cual se brindará el servicio pero con una menor calidad y con mayores probabilidades de apagones. Esta posibilidad hace necesario evaluar formas de tarifación que permitan que las familias paguen por el servicio que reciban y éste no vea deteriorada su calidad. El análisis de los impactos de una tarifa social será el tema de una nota posterior.
La Teoría de juegos
La teoría de juegos es un área de la matemática aplicada que utiliza modelos para estudiar interacciones en estructuras formalizadas de incentivos (los llamados juegos) y llevar a cabo procesos de decisión. Sus investigadores estudian las estrategias óptimas así como el comportamiento previsto y observado de individuos en juegos. Tipos de interacción aparentemente distintos pueden, en realidad, presentar estructuras de incentivos similares y, por lo tanto, representar conjuntamente un mismo juego.

Desarrollada en sus comienzos como una herramienta para entender el comportamiento de la economía, la teoría de juegos se usa actualmente en muchos campos, desde la biología a la filosofía. Experimentó un crecimiento sustancial y se formalizó por primera vez a partir de los trabajos de John von Neumann y Oskar Morgenstern, antes y durante la Guerra Fría, debido sobre todo a su aplicación a la estrategia militar —en particular a causa del concepto de destrucción mutua garantizada. Desde los setenta, la teoría de juegos se ha aplicado a la conducta animal, incluyendo el desarrollo de las especies por la selección natural. A raíz de juegos como el dilema del prisionero, en los que el egoísmo generalizado perjudica a los jugadores, la teoría de juegos se ha usado en ciencia política, ética y filosofía. Finalmente, ha atraído también la atención de los investigadores en informática, usándose en inteligencia artificial y cibernética.
Aunque tiene algunos puntos en común con la teoría de la decisión, la teoría de juegos estudia decisiones realizadas en entornos donde interaccionan. En otras palabras, estudia la elección de la conducta óptima cuando los costes y los beneficios de cada opción no están fijados de antemano, sino que dependen de las elecciones de otros individuos. Un ejemplo muy conocido de la aplicación de la teoría de juegos a la vida real es el dilema del prisionero, popularizado por el matemático Albert W. Tucker, el cual tiene muchas implicaciones para comprender la naturaleza de la cooperación humana. La teoría psicológica de juegos, que se arraiga en la escuela psicoanalítica del análisis transaccional, es enteramente distinta.
Los analistas de juegos utilizan asiduamente otras áreas de la matemática, en particular las probabilidades, las estadísticas y la programación lineal, en conjunto con la teoría de juegos. Además de su interés académico, la teoría de juegos ha recibido la atención de la cultura popular. La vida del matemático teórico laureado con un premio Nobel John Forbes Nash, desarrollador del Equilibrio de Nash, fue el tema de la biografía de Sylvia Nasar Una mente brillante (1998), y de la película del mismo nombre (2001). Varios programas de televisión han explorado situaciones de teoría de juegos, como el concurso de la televisión de Cataluña (TV3) Sis a traició (seis a traición), el programa de la televisión estadounidense Friend or foe? (¿Amigo o enemigo?) y, hasta cierto punto, el concurso Supervivientes.
Filosofía
La teoría de juegos ha demostrado tener muchos usos en filosofía. A partir de dos trabajos de W.V.O. Quine publicados en 1960 y 1967, David Lewis (1969) usó la teoría de juegos para desarrollar el concepto filosófico de convención. De esta forma, proporcionó el primer análisis del conocimiento común y lo empleó en analizar juegos de coordinación. Además, fue el primero en sugerir que se podía entender el significado en términos de juegos de señales. Esta sugerencia se ha seguido por muchos filósofos desde el trabajo de Lewis (Skyrms 1996, Grim et al. 2004).

Leon Henkin, Paul Lorenzen y Jaakko Hintikka iniciaron una aproximación a la semántica de los lenguajes formales que explica con conceptos de teoría de juegos los conceptos de verdad lógica, validez y similares. En esta aproximación los “jugadores” compiten proponiendo cuantificaciones e instancias de oraciones abiertas; las reglas del juego son las reglas de interpretación de las sentencias en un modelo, y las estrategias de cada jugador tienen propiedades de las que trata la teoría semántica –ser dominante si y sólo si las oraciones con que se juega cumplen determinadas condiciones, etc.-.
En ética, algunos autores han intentado continuar la idea de Thomas Hobbes de derivar la moral del interés personal. Dado que juegos como el dilema del prisionero presentan un conflicto aparente entre la moralidad y el interés personal, explicar por qué la cooperación es necesaria para el interés personal es una componente importante de este proyecto. Esta estrategia general es un componente de la idea de contrato social en filosofía política (ejemplos en Gauthier 1987 y Kavka 1986).
Finalmente, otros autores han intentado usar la teoría evolutiva de juegos para explicar el nacimiento de las actitudes humanas ante la moralidad y las conductas animales correspondientes. Estos autores han buscado ejemplos en muchos juegos, incluyendo el dilema del prisionero, la caza del ciervo, y el juego del trato de Nash para explicar la razón del surgimiento de las actitudes acerca de la moral (véase Skyrms 1996, 2004; Sober y Wilson 1999).
Descriptiva
El uso principal es informar acerca del comportamiento de las poblaciones humanas actuales. Algunos investigadores creen que encontrar el equilibrio de los juegos puede predecir cómo se comportarían las poblaciones humanas si se enfrentasen a situaciones análogas al juego estudiado. Esta visión particular de la teoría de juegos se ha criticado en la actualidad. En primer lugar, se la critica porque los supuestos de los teóricos se violan frecuentemente. Los teóricos de juegos pueden suponer jugadores que se comportan siempre racionalmente y actúan para maximizar sus beneficios (el modelo homo oeconomicus), pero los humanos reales a menudo actúan irracionalmente o racionalmente pero buscando el beneficio de un grupo mayor (altruismo).

Los teóricos de juegos responden comparando sus supuestos con los que se emplean en física. Así, aunque sus supuestos no se mantienen siempre, pueden tratar la teoría de juegos como una idealización razonable, de la misma forma que los modelos usados por los físicos. Sin embargo, este uso de la teoría de juegos se ha seguido criticando porque algunos experimentos han demostrado que los individuos no se comportan según estrategias de equilibrio. Por ejemplo, en el juego del ciempiés, el juego de adivinar 2/3 de la media y el juego del dictador, las personas a menudo no se comportan según el equilibrio de Nash. Esta controversia se está resolviendo actualmente.
Por otra parte, algunos autores aducen que los equilibrios de Nash no proporcionan predicciones para las poblaciones humanas, sino que proporcionan una explicación de por qué las poblaciones que se comportan según el equilibrio de Nash permanecen en esa conducta. Sin embargo, la cuestión acerca de cuánta gente se comporta así permanece abierta.
Algunos teóricos de juegos han puesto esperanzas en la teoría evolutiva de juegos para resolver esas preocupaciones. Tales modelos presuponen o no racionalidad o una racionalidad acotada en los jugadores. A pesar del nombre, la teoría evolutiva de juegos no presupone necesariamente selección natural en sentido biológico. La teoría evolutiva de juegos incluye las evoluciones biológica y cultural y también modela el aprendizaje individual.
Normativa
Por otra parte, algunos matemáticos no ven la teoría de juegos como una herramienta que predice la conducta de los seres humanos, sino como una sugerencia sobre cómo deberían comportarse. Dado que el equilibrio de Nash constituye la mejor respuesta a las acciones de otros jugadores, seguir una estrategia que es parte del equilibrio de Nash parece lo más apropiado. Sin embargo, este uso de la teoría de juegos también ha recibido críticas. En primer lugar, en algunos casos es apropiado jugar según una estrategia ajena al equilibrio si uno espera que los demás también jugarán de acuerdo al equilibrio. Por ejemplo, en el juego adivina 2/3 de la media.
El dilema del prisionero presenta otro contraejemplo potencial. En este juego, si cada jugador persigue su propio beneficio ambos jugadores obtienen un resultado peor que de no haberlo hecho. Algunos matemáticos creen que esto demuestra el fallo de la teoría de juegos como una recomendación de la conducta a seguir.

Historia de la teoría de juegos
La primera discusión conocida de la teoría de juegos aparece en una carta escrita por James Waldegrave en 1713. En esta carta, Waldegrave proporciona una solución minimax de estrategia mixta a una versión para dos personas del juego de cartas le Her. Sin embargo no se publicó un análisis teórico de teoría de juegos en general hasta la publicación de Recherches sur les principes mathématiques de la théorie des richesses, de Antoine Augustin Cournot en 1838. En este trabajo, Cournot considera un duopolio y presenta una solución que es una versión restringida del equilibrio de Nash.
Aunque el análisis de Cournot es más general que el de Waldegrave, la teoría de juegos realmente no existió como campo de estudio aparte hasta que John von Neumann publicó una serie de artículos en 1928. Estos resultados fueron ampliados más tarde en su libro de 1944, The Theory of Games and Economic Behavior, escrito junto con Oskar Morgenstern. Este trabajo contiene un método para encontrar soluciones óptimas para juegos de suma cero de dos personas. Durante este período, el trabajo sobre teoría de juegos se centró, sobre todo, en teoría de juegos cooperativos. Este tipo de teoría de juegos analiza las estrategias óptimas para grupos de individuos, asumiendo que pueden establecer acuerdos entre sí acerca de las estrategias más apropiadas.
En 1950, aparecieron las primeras discusiones del dilema del prisionero, y se emprendió un experimento acerca de este juego en la corporación RAND. Alrededor de esta misma época, John Nash desarrolló una definición de una estrategia óptima para juegos de múltiples jugadores donde el óptimo no se había definido previamente, conocido como equilibrio de Nash. Este equilibrio es suficientemente general, permitiendo el análisis de juegos no cooperativos además de los juegos cooperativos.

La teoría de juegos experimentó una notable actividad en la década de 1950, momento en el cual los conceptos base, el juego de forma extensiva, el juego ficticio, los juegos repetitivos, y el valor de Shapley fueron desarrollados. Además, en ese tiempo, aparecieron las primeras aplicaciones de la teoría de juegos en la filosofía y las ciencias políticas.
En 1965, Reinhard Selten introdujo su concepto de solución de los equilibrios perfectos del subjuego, que más adelante refinó el equilibrio de Nash. En 1967 John Harsanyi desarrolló los conceptos de la información completa y de los juegos bayesianos. Él, junto con John Nash y Reinhard Selten, ganaron el Premio Nobel de Economía en 1994.
En la década de 1970 la teoría de juegos se aplicó extensamente a la biología, en gran parte como resultado del trabajo de John Maynard Smith y su concepto estrategia estable evolutiva. Además, los conceptos del equilibrio correlacionado, la perfección del temblor de la mano, y del conocimiento común fueron introducidos y analizados.
En 2005, los teóricos de juegos Thomas Schelling y Robert Aumann ganaron el premio Nobel de Economía. Schelling trabajó en modelos dinámicos, los primeros ejemplos de la teoría de juegos evolutiva. Por su parte, Aumann contribuyó más a la escuela del equilibrio.
En el 2007, Roger Myerson, junto con Leonid Hurwicz y Eric Maskin, recibieron el premio Nobel de Economía por “sentar las bases de la teoría de diseño de mecanismos.”
Autores: Liliana Pereyra y Carlos Valquez (Instituto de Economía y Finanzas – Facultad de Ciencias Económicas – Universidad Nacional de Córdoba)
Fuentes: Wikipedia – Facultad de Ciencias Económicas – Universidad Nacional de Córdoba
Más información sobre Pérdidas No Técnicas
